q!An Application of AOC-Posets: Indexing Large Corpuses for Text Generation Under Constraints
Author Proof
B Alain Gutierrez, Michel Chein, Marianne Huchard, and Pierre Pompidor LIRMM, CNRS and Montpellier University, Montpellier, France mailto:{Alain.Gutierrez,michel.chein,marianne.huchard,pierre.pompidor}@lirmm.fr http://www.lirmm.fr
Abstract. In this paper, we describe the different ingredients of the CogiText tool which can be used for building, editing, and using large corpuses for text generation under constraints`alaAlamo. In CogiText, AOC-posets are used as indexes that give information about the shape of the corpuses and that help to efficiently find terms for the text creation process. We give some figures about their size and the needed time for computing them and for making a specific text creation.
Keywords: Formal concept analysis, AOC-poset, Text generation with constraints, Alamo
1 Introduction
OuLiPo [9] is a literary approach founded in 1960 by Raymond Queneau and François Le Lionnais that aims to create literary text with constraints in writing. In 1981, members of OuLiPo created Alamo [1], which is, as indicated by its name, a Workshop (Atelier in french) of Literature Assisted by Mathematics and Computers (Ordinateurs in french). Several tools were designed to assist this approach. In this paper, we introduceCogiText, which can be considered as the continuation of LAPAL (the last tool for automatic literary text creation developed within the framework of Alamo). CogiText contains tools for building, editing, or using large corpuses. For instance, the examples given in the paper are using corpuses built from DELA [5] for substantives (nouns) and adjectives, and from Morphalou [7] for verbs. Besides classical attributes e.g. gender) associated to each corpus item, phonetics has been obtained with an original software and can be used for computing metric properties (e.g. syllable number) or consonance properties (e.g. rhyme). For dealing with the large size of these corpuses, an original indexing method based on AOC-poset has been built. Another specificity is the use of a knowledge representation system enabling different ways to describe constraints: graphical interface, Datalog rules or Beanshell scripts. CogiText=CoGui + Text, where CoGui is a visual tool for building knowledge bases [4].
Springer International Publishing AG 2017 M. Kryszkiewicz et al. (Eds.): ISMIS 2017, LNAI 10352, pp. 1–11, 2017. OI: 10.1007/978-3-319-60438-163 A. Gutierrez et al.
Section 2 illustrates and outlines the approach, by showing an example of writing under constraints. Section 3 defines the corpuses and the phonetics. Production schemes are presented in Section 4. The use of AOC-posets for efficient indexing is detailed in Section 5. Section 6 describes the implementation and gives figures on the computation time of the AOC-posets and of the text production. We conclude in Section 7 with a few prospects of this work.
2 Motivation and Outline of the Approach
In this section, we illustrate the purpose of CogiText with a simple example. Let us assume that an author would like to produce a parody of the Jean de La Fontaine fable “le corbeau et le renard” (“the fox and the crow”). The title and the first two lines of the original text used to exemplify the approach are shown in the upper part of Table1. The design of this parody here is based on the definition of aproduction scheme including aproduction templateand a constraint set. We describe them here in a textual form, but a user interface is provided to assist the writer (see Sect. 6).
Table 1. Constraints inspired by the Jean de La Fontaine fable “Le corbeau et le renard”.
rhyme3 (resp.rhyme2) stands for rhymes with 3 (resp. 2) phonemes.
| First lines of the original text (French) | Translation (English) |
| Le corbeau et le renard | The crow and the fox |
| Maître Corbeau | Mister Crow |
| sur un arbre perché | perched on a tree |
| Tenait en son bec un fromage | was holding in his beak a cheese |
| Production template (french) | Production template (transposed) |
| Le {X1.txt} et le {X2.txt}. | The {X1.txt} and the {X_2_.txt}. |
| Maître {X1.txt}, | Mister {X1.txt}, |
| sur un {X3.txt} {X4.txt} | {X3.txt} on a {X4.txt} |
| Tenait en son {X5.txt} un {X6.txt} | was holding in its {X5.txt} a {X6.txt} |
| Constraint set (french) | Constraint set (transposed) |
| X1=element(corpusNoun) | X1=element(corpusNoun) |
| X1.rhyme3=”Rbo” | X1.rhyme2=”oW” |
| X1.nbsyl=2 | X1.nbsyl=1 |
| X1.gender=”masculine” | X1.gender=”neuter” |
| X1.number=”singular” | X1.number=”singular” |
| X2=element(corpusNoun) | X2=element(corpusNoun) |
| X2.rhyme3=”naR” | X2.rhyme1=”oX” |
| X2.nbsyl=3 | X2.nbsyl=1 |
| X3.gender=X4.gender | X3.gender=X4.gender |
| X3.number=X4.number; | X3.number=X4.number; |
The central part of Table 1 shows a production template for the parody. In the production template of the example, several words have been replaced by expressions referring to variables: here the text of the variable will be used to replace the initial word. Constraints are properties that the variables appearing in the production template should satisfy.
Table 2. Text productions for “Le corbeau et le renard”. The french text is automatically produced byCogiText. The english text is manually composed using the rhyming dictionary Rhymer [10] for making the technique understandable by english-speaking readers.
| Production (french) | Production (transposed) |
| Le barbot et le fouinard. | The woe and the vox. |
| Maitre barbot, | Mister woe, |
| sur un marbre torché, | lurched on a knee, |
| Tenait en son bec un dommage. | Holds in his creek a sneeze. |
The bottom part of Table1 shows a few constraints for “the fox and the crow” parody (see Appendix 2 for a more complete production scheme). From the "production scheme", and corpuses described in Sect. 3, CogiText builds "text productionsas" as the one shown in Table2 (left-hand-side). In productions, the expressions on variables are replaced by values. Here, the values are the texts of randomly chosen corpus elements that satisfy the constraints. For example, expression {X1.txt} is replaced by “barbot” which is a term found in the DELA lexicon [5], satisfying the constraints: noun, rhyme in “Rbo”, 2 syllables, singular, masculine.
The approach is outlined in Fig. 1: (1) the writer chooses corpuses among CogiText corpuses or builds his own corpuses (each term being equipped with attributes, key/value pairs, used in production schemes); (2) the writer types the production template and the constraints, that have to comply with the selected corpuses; (3) the system extracts the relevant key/value pairs on corpus elements (like gender="masculine", or rhyme3="Rbo") from the production scheme; (4) these key/value pairs are used to build indexes (with an AOC-poset structure); (5) corpus elements and values are randomly selected through AOC-poset; (6) the production is built by filling the expressions with the chosen element values; (7) the production is returned to the user.

Fig. 1. Outline of the approach
3 Corpuses and Phonetic Information
The approach requires significant linguistic resources to serve its purpose: corpuses that include a large set of terms with attributes, especially phonetics in our example since it concerns poetry.
CogiText Corpuses. CogiText is designed to work with any text corpus or lexicon, provided it is equipped with the structure that follows (examples of this paragraph are translated in English). A corpus is a set of elements.
A corpus element is a set of (key, value) pairs. For example, an element can be elem1= (txt, "home"), (rhyme2, "oM"), (gender, "neutral"), (nbsyl, 3), (syn, ["residence", "house"]). A key is simply a string, as txt (for “text”), rhyme2, gender, nbsyl (for “number of syllables”), syn (for “synonyms”). For example, for elem1, “home” is the value of key txt,3 is the value of nbsyl. The possible types of values are primitive types (string, integer, float, boolean) or arrays of these primitive types. Strings may include several words, lines, spaces or punctuation marks. Thus, if in our example the CogiText corpuses are lexicons, in other applications they can be corpuses in the usual linguistic meaning. A corpus schema is a structure for a corpus. It is composed of a set of (key, type) pairs. For the previous example, the corpus schema contains (txt, string), (rhyme2, string), (gender, string), (nbsyl, integer), (syn, array of string). A corpus element e complies with a corpus schema S if every (key, value) pair (k, v) is such that: if k appears in S, then it appears in at most one pair of e, and v is a value of its associated type in S (a corpus element does not necessarily contain all the keys of the schema). Several schemas can be associated with a given corpus. A corpus mapping associates a computed value with a corpus element. The mappings that return the values associated with a key are predefined. For example, e.txt is the mapping which associates to an element e the value associated with its key txt, e.g. elem1.txt="home". The null value is returned when the corpus element does not own this key. Other mappings can be defined by the user, in a dedicated language. For example, one can develop a mapping cutReturn6 that returns, for elements whose text has at least 6 characters, the string obtained by splitting the text into two parts and reversing these parts; e.g. if e.txt=“congratulate” e.cutReturn6 = "tulatecongra".
At this point CogiText contains three corpuses built from the french lexicons DELA (for nouns and adjectives) and Morphalou (for verbs). They are equipped with corpus schemas. DELA contains 102 073 lemmas, giving 683 824 inflected forms (including plural forms for example), and Morphalou introduces 8790 verb lemmas. An example of a DELA entry for a lemma is [précepteur, 1.N36(Hum)], where “précepteur” is the canonical
form, “1” is the lexical level, N36 is a morphological code which allows to calculate the different inflected forms, and “Hum” indicates that it applies to a human. An entry for an inflected form is: [préceptrice,précepteur. N36(Hum):fs], where “préceptrice” is the inflected form, “précepteur” is the canonical form, “fs” is the gender and the number (feminine, singular). Such information will appear in two corpus elements: p1 = (txt, "précepteur"), (gender, "masculine"), (nbsyl, 3), … and p2 = (txt, "préceptrice"), (gender, "feminine"), (nbsyl, 3)@@, …. The same principle applies to other categories. Details about the CogiText corpuses built from DELA and Morphalou are shown in Appendix 1.
Phonetic and Syllable Information. Phonetic syllabification of french words plays an important role in applications dealing with literary texts. The resources are composed of 641 handmade phonetic rules which come from the lexicon Descartes analysis [8] and a handmade lexicon of 1399 lemmas which have exceptional phonetics due to their exogenous origin. The tool has a few limitations, including: recognizing between the different forms of weak/mute “e” in french language is difficult; some ambiguous cases that would require a syntactic analysis are not considered; the pronounced liaison between the words is hard to know; and of course, the prosody is absent. Nevertheless 98.5% of the words are correctly pronounced. We illustrate our method on the verbal form “accéléraient” (as in “they accelerated” in English). The analysis is achieved in four steps:
– match with the longest phonetic suffix: ent| (matching with a verbal form) =>. (“e” is mute in “ent”, thus this is not considered as a phoneme)
– match with the longest phonetic prefix: |acc => ak-s+
– find intercalated phonemes: é => e,l => l+, é=>e, r=>r+, ai => E
– produce the final result: ak-s+|e|l+|e|r+|E|. => ak se le rE.
4 Production Scheme
A production scheme is composed of a production template and constraints.
A simple production template is a sequence of strings and expressions of the form {corpus.variable.corpusmapping}. A corpus variable is an identifier which represents an unknown corpus element. Each corpus variable refers to a
specific corpus, for example a variable may refer to the common noun corpus while another refers to the verb corpus. For example, production pattern “Le", expression {X1 et le {X2.txt}.” is a sequence composed of string “Le”@@, expression “{X1}”, string “et le”, expression {X2.txt}, and string “.”. The fact that variable X1 refers to the common noun corpus is the first constraint as noted in the constraint part of Table1.
A constraint is a property that variables appearing in a production template have to satisfy. They can be applied to a single variable as {X1.rhyme3="Rbo"} or they can apply to several variables as {X1.nbsyl = X2.nbsys1}. A constraint that applies to a single variable is a unary constraint. A unary constraint defines
a part of the corpus, for example {X1.nbsyl=2} amounts to considering only the common nouns that have two syllables, acting as a filter and limiting the number of the corpus elements that have to be considered. The binary constraints may involve different mappings, such as {X1.nbsyl = X2.nbvowels} and variables may refer to different corpuses: e.g. X1 may refer to a common noun and X2 may refer to a verb. We call simple constraints the constraints involving a relation = , =, <, or > between two unary mappings. Complex constraints can be defined (by programming) as {X1.nbsyl + X2.nbsyl + X3.nbsyl = 12}. The language is rather rich, enabling the use of standard functions that manipulate strings, as well as any user-defined function. The expression enclosed in braces {} can be: an expression that can be evaluated as a string, like {"hello"}, {"" + X1.nbsyl1 + "syllabes"}, {1+8}, {9}, or {"9"}; or the body of a function that returns a string, like {if("_masculine".equals(X1.gender)) return Le"; else return "La";}.
These templates and constraints are written using CoGui [4], which is a knowledge representation language. CoGui provides a graphical language for building conceptual graph knowledge bases [3] and allows us to define the constraints as predicates similar to Datalog rules.
5 Efficient Indexing and Text Production with AOC-Posets
A crucial step for efficiency of CogiText is a rapid access to the corpuses to find relevant corpus elements to be assigned to the corpus variables. This is achieved in three main steps: (1) An offline building of AOC-posets associated with the involved corpuses. These AOC-posets will be used as an index on the corpuses; (2) A computation of the needed key-value pairs for corpus variables from the constraints; (3) An assignment of corpus elements to variables using the AOC-posets of the variable corpus.
Offline Building of AOC-Posets. For each corpus, a general index is built, which takes the form of an AOC-poset associated with a formal context K=(O, A, R) where formal objects O are the corpus elements, formal attributes A are all the possible key-value pairs according to the corpus schema, and R ⊆ O × A associates a corpus element to a key-value pair it owns. The concepts built on top of K are pairs of sets (E, I) such that E ⊆ O and I ⊆ A. E is a maximal set of formal objects (extent) associated with the maximal set I of formal attributes (intent) they share [6]. They are organized by inclusion of their extent in the concept lattice, giving a specialisation order ≤. C1 ≤ C2 if and only if E1 ⊆ E2 and I2 ⊆ I1. C1 is a subconcept of C2 and C2 is a superconcept of C1. A concept C introduces a formal attributea a (resp. a formal object o) if C is the highest (resp. lowest) concept in ≤ with a in its intent (resp.o in its extent). The AOC-poset is the suborder of the concept lattice restricted to the concepts that introduce at least one formal attribute, or one formal object. Specialized algorithms for building AOC-posets are presented in [2]. Compared to the concept lattice, whose concept number can reach 2min(|O|,|A|), the AOC-poset concept number is limited to |O| + |A|.
Table 3. Partial formal context for the corpus built upon DELA nouns
| Offset (text) × key-value | gender _masculine | number _singular | nbsyl 1 | nbsyl | nbsyl 3 | rhyme3 naR | rhyme3 Rbo | rhyme3 RbR | rhyme3 maZ | rhyme3 bEk | … |
| 164555 (renard) | x | x | x | x | … | ||||||
| 348 (fouinard) | x | x | x | x | … | ||||||
| 110976 (corbeau) | x | x | x | x | … | ||||||
| 345724 (barbot) | x | x | x | x | … | ||||||
| 734657 (turbo) | x | x | x | x | … | ||||||
| 12456 (arbre) | x | x | x | x | … | ||||||
| 78347 (marbre) | x | x | x | x | … | ||||||
| 1110723 (bec) | x | x | x | x | … | ||||||
| 34677 (fromage) | x | x | x | x | … | ||||||
| 125044 (dommage) | x | x | x | x | … | ||||||
| ……… | … |
Table 3 shows a part of the formal context for the corpus built upon the DELA nouns. The shown part of the table focuses on some corpus elements and key-value pairs useful to illustrate our approach. Figure 2 (left-hand side) shows a table (restricted to the key-value pairs used in “Le corbeau et le renard” example: e.g. gender="_masculine", number="_singular", nbsyl=1), which allows a rapid access to the AOC-poset. Figure 2 (central part) shows the AOC-poset associated with the shown part of the formal context of Table 3. For the whole corpus, the AOC-poset is of course larger and has a different shape. Offsets are pointers towards the data files that enable to efficiently access from a concept extent to corpus data files (links from center to right-hand side of Fig. 2).
Computation of Key-Value Pairs for Corpus Variables. The second step computes the key-value pairs for the corpus variables of the production scheme. The equalities are used to group equal expressions. For example if the constraints
are X1.gender=X2.gender and X1.gender="masculine", then X1.gender,
X2.gender and "masculine" are grouped. If the group contains a single value, this value is assigned to the expressions. If the group contains several different values, the group is inconsistent and no solution can be found. This may happen if, for example, to the previous constraints we add:X2.gender="feminine".
A group may only contain expressions (and no fixed value). For example, a hypothetical group may only contain X3.nbsyl and X4.nbvowels, due to a
given constraint X3.nbsyl = X4.nbvowels and the fact that no other constraint gives a value neither to X3, nor to X4. In this case, a value has to be randomly chosen. Each expression of the group has a set of possible values in the associated variable corpus, for example X3 could come from the DELA noun corpus, and
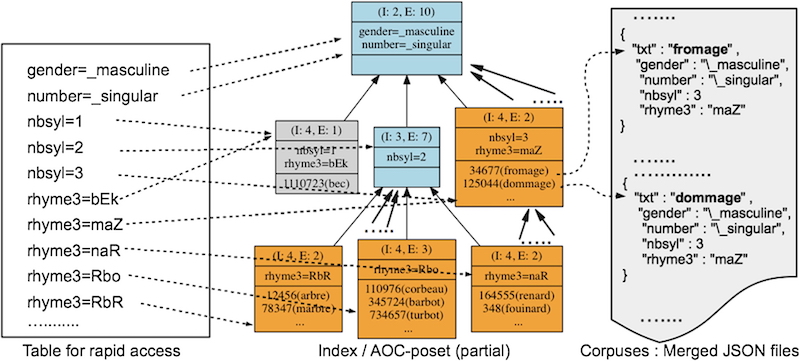
Fig. 2.Partial AOC-poset for partial formal context of Table 3. “I” stands for intent and is followed by the intent size (number of formal attributes); “E” stands for extent and is followed by the extent size (number of formal objects).
X3.nbsyl can take values in {1,2, ...14}, while X4 could come from the DELA adjective corpus and X4.nbvowels can take values in {1,2, ...6}. The intersection of the value sets is computed. For the example, this intersection is {1,2, ...14} ∩ {1,2, …6} = {1,2, …6}. The AOC-posets associated with the corpuses allow to count how many corpus elements own each value of the intersection. A value is randomly chosen with a weighted sampling based on the number of relevant corpus element tuples. E.g. for computing this number in the previous example, to each value x of {1,2, ...6}, we associate the number of (noun, adjective) pairs such that the noun has x syllables and the adjective has x vowels.
Assignment of Corpus Elements to Variables. After the previous step, all expressions relative to a variable have a value. These key-value pairs determine one or more concepts (the highest concepts containing all these key-value pairs) which exist if corpus elements exist with these values. For each variable, a corpus element is randomly selected in the union of the extents of the concepts that own all the key-value pairs associated with this variable. In the simplified example of “Le corbeau et le renard” parody, for each set of constraints on a variable, a single concept (introducing the initial word) has the whole set of key-value pairs of the variable, but this is a specific case. A selection in this case is simple, e.g. the noun corpus element with text “barbot” can be randomly chosen in the extent of the concept introducing “corbeau” and assigned to X1 of Table 1.
6 Implementation
Implementation Framework. CogiText enhances the Cogui environment and provides a graphical interface for easy typing of production templates and constraints (see Fig. 3 which shows a graphical window for constraint editing).

Fig. 3. Graphical description of the variable X1 (called CORBEAU in the interface) constraints.
The two corpuses DELA and Morphalou are equipped with corpus schemas as explained in Sect. 3 and are encoded in JSON (JavaScript Object Notation) which is a lightweight data-interchange format, readable by humans and easy to automatically parse. The corpuses are stored in concatenated JSON files to ensure an efficient access to corpus elements via integers that serve as pointers.
Size and Computation Time. Table 4 shows the size and the computation time for AOC-posets associated with the “Le corbeau et le renard” parody and the DELA noun corpus. The AOC-posets are built without filtering, or with a filtering which consists in keeping the key-value pairs useful for answering to the query and the corpus elements which have at least one of these key-value pairs.
Several algorithms have been applied, using two different Java implementations for each of them: one using the JavaBitSetdata structure and one using the Java HashSet data structure. For these data and the BitSet implementation, CERES is the most efficient, e.g. running within 1 s for the filtered data (3-phonemes) and within 4 min for the whole data (3-phonemes). For the HashSet implementation, CERES remains competitive, but in the filtered cases, PLUTON is the best.
The AOC-posets are built offline. For our example, AOC-posets are built for the DELA noun and adjective corpuses.
Then the time t for a text production is:
- For a 3-phonemes search (#possibilities: X1:7, X2:27, X3:2, X4:3, X5:1, X6:27)
- with the filtered data:t= 787 ms, including 3 ms needed to traverse the AOC-posets (for getting the whole concept extents in which a corpus element is randomly chosen).
- with the non filtered data:t= 1571 ms, including a 37 ms traversal.
- For a 2-phonemes search (#possibilities: X1:37, X2:494, X3:16, X4:27, X5:13 X6:682)
- with the filtered data:t= 761 ms, including a 12 ms traversal.
- with the non filtered data:t= 692 ms, including again a 12 ms traversal.
Table 4. Size and computation time of AOC-posets for DELA nouns
key-value pairs for rhyme3+nbsyl+gender+number with filtering
| #elements | #key-value pairs | density | building matrix ex. time | #concepts |
| 137276 | 10 | 0.17 | 50s | 56 |
| Time | CERES(ms) | PLUTON(ms) | HERMES(ms) | ARES(ms) |
| BitSet | 1229 | 2057 | 3124 | 26445 |
| HashSet | 1327 | 425 | 85887 | 36186 |
key-value pairs for rhyme2+nbsyl+gender+number with filtering
| #elements | #key-value pairs | density | building matrix ex. time | #concepts |
| 137413 | 10 | 0.17 | 50s | 85 |
| Time | CERES(ms) | PLUTON(ms) | HERMES(ms) | ARES(ms) |
| BitSet | 1315 | 2427 | 3478 | 31350 |
| HashSet | 1329 | 388 | 78500 | 31671 |
key-value pairs for rhyme3+nbsyl+gender+number without filtering
| #elements | #key-value pairs | density | building matrix ex. time | #concepts |
| 160268 | 4800 | 8.32E-4 | 50s | 33669 |
| Time | CERES(ms) | PLUTON(ms) | HERMES(ms) | ARES(ms) |
| BitSet | 216152 | 1884040 | 1422808 | 4018082 |
| HashSet | 138069 | 400936 | 580275 | 3635452 |
key-value pairs for rhyme2+nbsyl+gender+number without filtering
| #elements | #key-value pairs | density | building matrix ex. time | #concepts |
| 160268 | 627 | 6.32E-3 | 50s | 7999 |
| Time | CERES(ms) | PLUTON(ms) | HERMES(ms) | ARES(ms) |
| BitSet | 7839 | 145148 | 179065 | 455852 |
| HashSet | 3229 | 22700 | 122855 | 729366 |
7 Conclusion
We presented an approach that assists the generation of literary texts with the support of corpuses equipped with corpus schemas, production schemes (composed of production patterns and constraints) and AOC-posets that provide information on the corpus structure (e.g. for choosing values for non-valued variable keys) and allow an efficient access for filling the corpus variables and the production patterns. The results show the benefits of the approach in a realistic case. As a future work, we would like to consider more complex constraints, e.g. inequalities or differences between variable key-values and also constraints expressed as predicates satisfying a set of DATALOG + rules. We also would like to investigate a process systematically including an on-the-fly generation of AOC-posets specialized for a specific production scheme.
Acknowledgments. The authors warmly thank Guy Chaty who introduced them in the ALAMO world.
References
- ALAMO: Workshop (Atelier in French) of Literature Assisted by Mathematics and Computers (Ordinateurs in French) (1981). http://www.alamo.free.fr/. Accessed 01 Jan 2017
- Berry, A., Gutierrez, A., Huchard, M., Napoli, A., Sigayret, A.: Hermes: a simple Proofand efficient algorithm for building the AOC-poset of a binary relation. Ann. Math.Author Artif. Intell.72(1–2), 45–71 (2014)
- Chein, M., Mugnier, M.L.: Graph-Based Knowledge Representation: Computational Foundations of Conceptual Graphs, 1st edn. Springer Publishing Company (2008, incorporated)
- CoGui: Visual tool for building conceptual graph knowledge bases (2008). http://www.lirmm.fr/cogui/. Accessed 01 Jan 2017
- DELA: (dictionnaires/lexicons). LADL (Laboratoire d’Automatique Documentaire et Linguistique)- now in Institut Gaspard Monge (IGM). http://infolingu.univ-mlv.fr/. Accessed 01 Jan 2017
- Ganter, B., Wille, R.: Formal Concept Analysis - Mathematical Foundations. Springer, Heidelberg (1999)
- Morphalou: (lexique/lexicon). laboratoire ATILF (Nancy Universit´e-CNRS). http://www.cnrtl.fr/lexiques/morphalou/LMF-Morphalou.php. Accessed 01 Jan 2017
- New, B., Pallier, C., Brysbaert, M., Ferrand, L.: Lexique 2: a new French lexical database. Behav. Res. Methods Instrum. Comput.36(3), 516–524 (2004)
- OuLiPo: Ouvroir de Littérature Potentielle (“workshop of potential literature”(1961). http://www.oulipo.net/. Accessed 01 Jan 2017
- Rhymer: Rhyming Dictionary, WriteExpress. http://www.rhymer.com/RhymingDictionary/. Accessed 01 Jan 2017
